Before I even start talking about linked lists in this post, I would like to strongly point out how important algorithms and data structures are. This is something a software engineer uses literally 100% of the time, even if we are talking about the simplest possible task. It is essential for someone to understand what algorithm complexity means and how it can affect their code and more importantly – the quality and the performance of their program.
This topic is extensively covered by tens or even hundreds of books, university courses and job interviews. If you know how to develop some clever algorithms and data structures, you will be a much more wanted person for any company out there.
The information in this section is in place for absolutely every algorithms and data structures related post I write, so I won’t repeat myself every single time. Just remember:
Algorithms and data structures are essential!
What is a linked list?
A linked list is a data structure that consists of ordered elements, linked between each other using pointers. The next figure shows a diagram of a linked list:

The next snippet of code shows how the linked list can be represented in C or C++:
typedef int item_type;
typedef struct list {
item_type item;
struct list *next;
} list;Here is how the same thing can be achieved in Java:
/**
* Represents a list node.
* @author Ivan Nikolov
*
*/
public class Node {
private int data;
private Node next;
public int getData() {
return this.data;
}
public void setData(int data) {
this.data = data;
}
public void setNext(Node next) {
this.next = next;
}
public Node getNext() {
return this.next;
}
}/**
* A class that represents a list
*
* @author Ivan Nikolov
*
*/
public class List {
private Node first;
public List() {
this.first = null;
}
}The Java code is much more for the same thing and it requires two classes, but you will see why further in the article. For now it’s important to say that to avoid repetition, all the Java functions shown further should be added to the List class.
Operations over data structures
Every time we talk about data structures, there are three main operations:
- Insertion
- Deletion
- Search
These operations differ for the different data structures and they are one of the main factors that determine which data structure to use.
Insertion
The insertion in linked lists is a constant time operation. It is as simple as adding a new element to the beginning of the list and modifying the head pointer to point to the new element. The next figure shows how it looks like:
void insert_item(list **l, item_type item) {
list *element = (list *)malloc(sizeof(list));
element->item = item;
element->next = *l;
*l = element;
}The same thing in Java looks like this:
public void insert(int data) {
Node node = new Node();
node.setData(data);
node.setNext(first);
first = node;
}Can you feel the expressive power of C/C++?
Search
The search operation was mentioned after the deletion above, but here I am representing it before. You will see why in a bit.
Finding an element in a linked list has linear time complexity, because in the worst case we will iterate over all elements until we find/not find what we’re looking for. Again and as before, there is the C or C++ code for this:
list *find_element(list *l, item_type i) {
if (l == NULL) return NULL;
if (l->item == i) return l;
return find_element(l->next, i);
}And the Java code:
public Node find(int i) {
return find(first, i);
}
private Node find(Node node, int i) {
if (node == null) return null;
if (node.getData() == i) return node;
return find(node.getNext(), i);
}The reason to implement the Java code with two methods was just to get a similar implementation working good for the object-oriented nature of Java. Otherwise both C/C++ and Java can implement this method iteratively rather than recursively and the final results will be exactly the same (in terms of complexity and returned value).
Deletion
The deletion is the tricky part in linked lists. It consists of a few steps:
- Finding the element before the one we want to delete.
- Changing its pointer to the one after the element we want to delete.
- Finally deleting the element.
The deletion itself is a quick operation and it’s much better than when it’s done with arrays. There everything that’s on the right of the deleted element has to be shifted. However, it is still linear time complexity, because of the search.
The deletion is shown in the next figure:
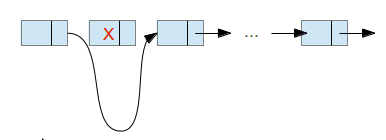
There are some special cases that we need to take care of. Most importantly – when the element we want to delete is the first one.
Now the C/C++ implementation follows:
//needed for deletion.
list *find_predecessor(list *l, item_type i) {
//didn't find
if (l == NULL || l->next == NULL) return NULL;
//the current one is the predecessor
if ((l->next)->item == i) return l;
return find_predecessor(l->next, i);
}
void delete_element(list **l, item_type i) {
//here we need double pointer, because addresses are passed by value and even if we can change
//the contents of the address, we cannot change the address itself. We will need to do this when we
//delete the first element...
if (l == NULL) return;
list *el = find_element(*l, i);
list *pred;
if (el) {
printf("Deleting %d\n", i);
pred = find_predecessor(*l, i);
if (pred) {
pred->next = el->next;
} else {//first element...
*l = el->next;
}
free(el);
}
}The Java version looks like this:
public Node findPredecessor(int i) {
return findPredecessor(first, i);
}
private Node findPredecessor(Node node, int i) {
if (node == null || node.getNext() == null) return null;
if (node.getNext().getData() == i) return node;
return findPredecessor(node.getNext(), i);
}
public void delete(int i) {
Node element = find(i);
if (element != null) {
Node predecessor = findPredecessor(i);
if (predecessor != null) {
predecessor.setNext(element.getNext());
} else {
first = element.getNext();
}
element = null;
}
}The way we have implemented it, we have to find the element to be deleted first and then find its predecessor. However, there is room for optimization only with one linear scan.
Conclusion
I presented the linked list data structure in this post, together with some of the most common operations over it. Additionally, it won’t be hard to implement finding an element by its index (not value) and enhancing the lists by adding size counters, for example. In some of the future posts I will show more operations over linked lists, that might be helpful to those, who are preparing for an interview.
Now, whenever you use standard Java (or whatever language you think of) lists, you will know what actually happens behind the scenes!
Thanks for reading!
