In this article I will present trees. This is another data structure that is really important in computer science and it can be used to model different relationships between real life objects. It could be also helpful as a data structure for some algorithms and also as a base of other data structures like maps or sets for example (tree maps/tree sets).
Binary trees
Before we even start looking into trees, let’s define a few terms that are important in understanding this data structure:
- Parent – this is the direct ancestor of a node in a tree.
- Child – the direct successor of a node in a tree.
- Ancestor
- Successor
The purest form of a tree is a data structure, which has one parent node, called root. The root has a number of children, which in turn could have more children and so on.
I will be presenting binary trees, because they have some interesting properties, but the algorithms shown here can also be applied to arbitrary trees with some changes. Binary trees have the following features:
- Every node in the tree has up to two children.
- The value of the left child is smaller than the value of the parent.
- The value of the right child is bigger than the value of the parent.
The next figure shows a binary tree:
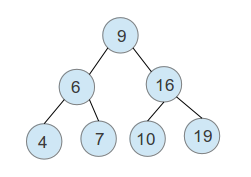
The tree in this figure is balanced, but it is not a requirement for the binary tree. However, this is a desired property for any tree, because it allows tree-based algorithms to have optimal performance.
The next piece of code will present the structure of a binary tree in C/C++:
typedef int item_type;
typedef struct tree {
item_type item;
struct tree *parent;//optional
struct tree *left;
struct tree *right;
} tree;Here is how the same structure will look in Java:
/**
* Represents a tree node.
*
* @author Ivan Nikolov
*
*/
public class Node {
private int data;
private Node left;
private Node right;
private Node parent;
public int getData() {
return this.data;
}
public void setData(int data) {
this.data = data;
}
public Node getLeft() {
return this.left;
}
public void setLeft(Node left) {
this.left = left;
}
public Node getRight() {
return this.right;
}
public void setRight(Node right) {
this.right = right;
}
public Node getParent() {
return this.parent;
}
public void setParent(Node parent) {
this.parent = parent;
}
}/**
* Represents a tree.
* @author Ivan Nikolov
*
*/
public class Tree {
private Node root;
public Tree() {
this.root = null;
}
}Operations over the binary tree
There are a few main operations one can perform over the binary tree.
- Insertion
- Deletion
- Search
- Traversal – this one is additional to the main three from all data structures.
Let’s have a look at these operations in the following sub-sections.
Insertion
Inserting an element in a binary tree is an operation that takes logarithmic time in terms of the tree size (logn). It is a really interesting operation, because each element in the binary tree has a well defined position, so we first need to find where it has to go and then put it there.
Here is how we would do this in C/C++:
void insert_tree(tree **t, item_type item, tree *parent) {
tree *p;
if (*t == NULL) {
p = (tree *)malloc(sizeof(tree));
p->left = p->right = NULL;
p->parent = parent;
p->item = item;
*t = p;
return;
}
if (item < (*t)->item) {
insert_tree(&((*t)->left), item, *t);
} else {
insert_tree(&((*t)->right), item, *t);
}
}The same code in Java will look like this:
public void insert(int data) {
root = insert(root, data, null);
}
private Node insert(Node current, int data, Node parent) {
if (current == null) {
current = new Node();
current.setData(data);
current.setLeft(null);
current.setRight(null);
current.setParent(parent);
} else if (data < current.getData()) {
current.setLeft(insert(current.getLeft(), data, current));
} else {
current.setRight(insert(current.getRight(), data, current));
}
return current;
}As you can see, the insertion in a binary tree is a recursive operation, which will make sure the element we’re adding will be exactly at the right place.
Balancing a tree
Earlier, when we showed the example figure of a tree, we mentioned that it is a balanced one. If you look at the code above, you might notice that if we insert elements in a descending or ascending order, the tree will end up having respectively only left or right children. This would effectively make all operations linear and our tree will behave like a linked list. We will end up losing all the good features of trees.
That’s why, when working with binary trees, one must either be aware of how the items are inserted, or perform a balancing operation from time to time. Balancing a tree and balanced trees are outside of the scope of this post, but you should be aware of this and you can look it up if needed.
Search
Now comes time for the search operation in a binary tree. It really looks like the insertion and it takes logarithmic time (logn). This is for a well balanced tree, of course!
The C/C++ code looks like the following:
tree *search_tree(const tree *t, item_type i) {
if (t == NULL) return NULL;
if (t->item == i) return t;
if (i < t->item) {
return search_tree(t->left, i);
} else {
return search_tree(t->right, i);
}
}The Java representation of the above code looks like this:
public Node find(int data) {
return find(root, data);
}
private Node find(Node current, int data) {
if (current == null)
return null;
if (current.getData() == data)
return current;
return find(data < current.getData() ? current.getLeft() : current.getRight(), data);
}Searching for min and max
The binary tree has some interesting features allowing us to find special elements in the tree quite easily. For example, the minimum and maximum elements. The minimum value is the leftmost child and the maximum is the rightmost.
Here is the code for finding minimum in C/C++:
tree *find_min(const tree *t) {
if (t == NULL) return NULL;
tree *min = t;
while (min->left != NULL) {
min = min->left;
}
return min;
}The Java code looks like the following:
public Node findMin() {
Node min = root;
if (min == null) return null;
while (min.getLeft() != null) {
min = min.getLeft();
}
return min;
}Deletion
Deleting an element of a tree is the hardest operation that we will look into. However, it also takes logn time. There are a few situations one has to handle:
- Deleting an element without any children – just free the memory.
- Deleting an element with only one child – change the pointers from the parent straight to the child and free the memory.
- Deleting an element with only one child and this is the ROOT element – move the child to the root and free the memory.
- Deleting an element with two children – this is the trickiest operation. The best way to handle it is to swap the values of the element to be deleted and the maximum value of the left subtree or the minimum value of the right subtree (because this will keep the features of the tree) and then delete an element without any or with one child.
Here is how we would implement deletion from a binary tree in C/C++:
void delete_element(tree **t, item_type item) {
if (t == NULL) return;
tree *element = search_tree(*t, item);
if (element == NULL) return;
int hasParent = element->parent != NULL;
int isLeft = hasParent && element->item < element->parent->item;
if (element->left == NULL && element->right == NULL) {//no children
if (hasParent) {
if (isLeft) {
element->parent->left = NULL;
} else {
element->parent->right = NULL;
}
}
free(element);
} else if (element->left != NULL && element->right == NULL) {//only left child
element->left->parent = element->parent;//even if it does not have a parent it will be cool
if (hasParent) {
if (isLeft) {
element->parent->left = element->left;
} else {
element->parent->right = element->left;
}
} else {
*t = element->left;
}
free(element);
} else if (element->left == NULL && element->right != NULL) {//only right child
element->right->parent = element->parent;
if (hasParent) {
if (isLeft) {
element->parent->left = element->right;
} else {
element->parent->right = element->right;
}
} else {
*t = element->right;
}
free(element);
} else {//it has two children...
//find the minimum of the right subtree and relabel the current element with it + delete the newly found element.
tree *right_min = find_min(element->right);
element->item = right_min->item;//relabel
//delete the new minimum
delete_element(&right_min, right_min->item);
}
}Let’s now see the Java implementation:
public void delete(int data) {
root = delete(root, data);
}
private Node delete(Node startNode, int data) {
Node element = find(startNode, data);
if (element == null) return startNode;
boolean hasParent = element.getParent() != null;
boolean isLeft = hasParent && element.getData() < element.getParent().getData();
if (element.getLeft() == null && element.getRight() == null) {
if (hasParent) {
if (isLeft) {
element.getParent().setLeft(null);
} else {
element.getParent().setRight(null);
}
}
} else if (element.getLeft() != null && element.getRight() == null) {
if (hasParent) {
if (isLeft) {
element.getParent().setLeft(element.getLeft());
} else {
element.getParent().setRight(element.getLeft());
}
} else {
startNode = element.getLeft();
}
} else if (element.getLeft() == null && element.getRight() != null) {
if (hasParent) {
if (isLeft) {
element.getParent().setLeft(element.getRight());
} else {
element.getParent().setRight(element.getRight());
}
} else {
startNode = element.getRight();
}
} else {
Node rightMin = findMin(element.getRight());
element.setData(rightMin.getData());
return delete(rightMin, rightMin.getData());
}
element = null;
return startNode;
}Both implementations are equivalent. The Java one is more object-oriented, while the C/C++ one is more like you would write it in a procedural language. It’s up to personal preferences which one would be preferred when learning new concepts.
Tree traversal
Traversal of a tree is the process of walking over all the nodes of the tree and processing them accordingly. There are three traversal types for binary trees:
- Inorder – visit the left subtree, the root and the right subtree.
- Preorder – visit the root, the left subtree and the right subtree.
- Postorder – visit the left subtree, the right subtree and the root.
Here is the output of each of those traversals over the tree shown in the next figure:



- Inorder – 4, 6, 7, 9, 10, 16, 19. As you can see, for binary trees this traversal outputs the values sorted. This is a really useful feature.
- Preorder – 9, 6, 4, 7, 16, 10, 19.
- Postorder – 4, 7, 6, 10, 19, 16, 9.
Let’s see some code, which implements the binary tree traversal in C/C++:
typedef enum traversal_type {
INORDER,
PREORDER,
POSTORDER
} traversal_type;
void traverse_tree(const tree *t, traversal_type trav_type) {
if (t == NULL) return;
switch (trav_type) {
case INORDER:
traverse_tree(t->left, trav_type);
process_node(t->item);
traverse_tree(t->right, trav_type);
break;
case PREORDER:
process_node(t->item);
traverse_tree(t->left, trav_type);
traverse_tree(t->right, trav_type);
break;
case POSTORDER:
traverse_tree(t->left, trav_type);
traverse_tree(t->right, trav_type);
process_node(t->item);
break;
}
}Here is the same thing, written in Java:
/**
* Represents traverse types available for a binary tree.
* @author Ivan Nikolov
*
*/
public enum TraverseType {
INORDER,
PREORDER,
POSTORDER;
}public void traverseTree(TraverseType traverseType) {
traverseTree(root, traverseType);
System.out.println();
}
private void traverseTree(Node current, TraverseType traverseType) {
if (current == null)
return;
switch (traverseType) {
case INORDER:
traverseTree(current.getLeft(), traverseType);
processNode(current);
traverseTree(current.getRight(), traverseType);
break;
case PREORDER:
processNode(current);
traverseTree(current.getLeft(), traverseType);
traverseTree(current.getRight(), traverseType);
break;
case POSTORDER:
traverseTree(current.getLeft(), traverseType);
traverseTree(current.getRight(), traverseType);
processNode(current);
break;
}
}Conclusion
This article presented binary trees with some operations over them and some of their interesting features. Many of the approaches used here can be easily transferred to arbitrary trees.
Of course, it is worth mentioning that nowadays all those algorithms are already implemented for us in the standard libraries of most modern languages. However, it is good to be familiar with their specifics and knowing what might be happening behind the scenes.
Have fun exploring trees and their power when creating your applications!
