Before we start discussing the topic of this post, we need to point out how important sorting actually is. Almost every problem that one will face in computer science can be solved with sorting as an initial phase. That’s why everybody must know a few good sorting techniques and when they can be used.
Let’s not even consider bubble sort and other algorithms with sqr(n) complexity as this is way too much especially with the amounts of data we see nowadays. If someone gets asked a question with sorting on a job interview, please don’t reply bubble sort! Of course, it is good knowing about it, but there are methods, which are much more suitable.
In this article I will present heap sort, which is one of my favourite sorting algorithms. You will see why and how it is implemented in the following sections.
Heap
The heap sort, as the name suggests, uses a heap. But what is a heap? This is a really interesting data structure, which can represent a tree-like structure in an array. Let’s take a look at the tree I have shown in one of my previous blog posts:
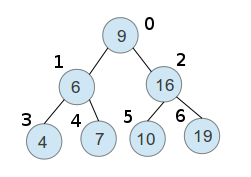
I have just indexed the elements as they are seen in the tree. If you take a closer look at the numbers, you will see a really interesting pattern:
The children of an element with index
iare with indexes2i + 1and2i + 2. There is also an easy way to find out the parent of an element, but I am leaving that to you to get to, based on what I already said.
This is exactly how a binary tree can be represented in an array. However, there is one more really important requirement here: the tree must be balanced or at least no elements should be missing (e. g. if we want to have leaves 5 and 6 in our figure, 3 and 4 must also be in the tree).
Now the tree in the previous figure will look as follows if represented as an array:
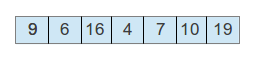
Those of you, who are familiar with heaps, however, will say that this is not an actual heap. And you will be correct. To have a real heap, we need to slightly change the properties of the binary tree that we had.
In a heap, the properties are that the parent element is smaller/larger than its both children. It is smaller in the so called min-heap and larger in a max-heap. So, after we heapify our tree, we will have the following min heap:
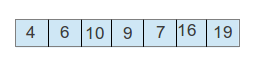
Since we have a min heap, we are sure that the first element is the smallest one. If we had a max heap, the first element would have been the biggest one.
The algorithm
After presenting the heap data structure, some of you might have already got the idea. The heap sort algorithm is one based on a data structure. A heap can also be used to represent a priority queue, for example. Here are the steps that we have to take in order to perform heap sort:
- Heapify the array (depending on the order ascending or descending, it will be max or min heap).
- Remove the first element from the array as it is sorted by swapping it with the last one and making the heap one element smaller.
- Go to 1.
The first heapification is the harderst one. All consecutive ones are done just to rearrange the elements in a way that the next correct comes in place.
Some interesting details about the approach I will show are that:
- A max heap is used for ascending order and a min heap for descending. This sounds inverted, but you will see why in the next point.
- When removing the first element and swapping it with the last one, the size of the heap is decremented from the back and this way we can use all the same index arithmetics.
Let’s go to the interesting part now – the code. Here is the representation in C/C++:
typedef int item_type;
typedef enum sort_order {
ASCENDING,
DESCENDING
} sort_order;
//we can have more optimal implementation only with pointers here!
void swap(item_type *arr, unsigned int a, unsigned int b) {
if (a == b) return;
item_type tmp = arr[a];
arr[a] = arr[b];
arr[b] = tmp;
}
void heap_sort(item_type *arr, unsigned int n, sort_order order) {
unsigned int i;
make_heap(arr, n, order);
for (i = 0; i < n - 1; i++) {
swap(arr, 0, n - 1 - i);//swap the first with the last - the last slides down. With min heap we will have a descending sort.
heapify(arr, n - i - 1, 0, order);
}
}
void make_heap(item_type *arr, unsigned int n, sort_order order) {
if (n <= 1) return; //nothing to do. int i; //assume the leaves are normal heaps!!! for (i = (n-2)/2; i >= 0; i--) heapify(arr, n, i, order);
}
//restores the heap properties for the element at index.
void heapify(item_type *arr, unsigned int n, unsigned int index, sort_order order) {
if (index >= n) return;
unsigned int min_max = index;
unsigned int left = index * 2 + 1;
unsigned int right = index * 2 + 2;
if (left < n && (order == DESCENDING ? arr[min_max] > arr[left] : arr[min_max] < arr[left])) min_max = left;
if (right < n && (order == DESCENDING ? arr[min_max] > arr[right] : arr[min_max] < arr[right])) min_max = right;
//the order has changed
if (min_max != index) {
swap(arr, index, min_max);
heapify(arr, n, min_max, order);
}
}Here is the same implementation, but in Java:
**
* Represents a sort order.
*
* @author Ivan Nikolov
*
*/
public enum SortOrder {
ASCENDING,
DESCENDING;
}import java.util.ArrayList;
/**
* A class representing a heap.
*
* @author Ivan Nikolov
*
*/
public class Heap {
private ArrayList items;
private SortOrder order;
/**
* Creates a heap from an array of integers.
*
* @param data The initial data.
*/
public Heap(ArrayList data, SortOrder order) {
//don't modify the input array list
ArrayList inputData = new ArrayList(data.size());
inputData.addAll(data);
inputData = makeHeap(inputData, inputData.size(), order);
this.items = inputData;
this.order = order;
}
private ArrayList makeHeap(ArrayList data, int size, SortOrder order) {
if (data == null || size <= 1) {
return data;
}
for (int i = (data.size() - 2)/2; i >= 0; i--) {
heapify(data, size, i, order);
}
return data;
}
private void heapify(ArrayList data, int size, int i, SortOrder order) {
if (data == null || i >= size) {
return;
}
int min_max = i;
int left = 2*i + 1;
int right = 2*i + 2;
if (left < size && (order == SortOrder.ASCENDING ? data.get(min_max) < data.get(left) : data.get(min_max) > data.get(left))) {
min_max = left;
}
if (right < size && (order == SortOrder.ASCENDING ? data.get(min_max) < data.get(right) : data.get(min_max) > data.get(right))) {
min_max = right;
}
if (min_max != i) {
swap(data, min_max, i);
heapify(data, size, min_max, order);
}
}
private void swap(ArrayList arr, int a, int b) {
int temp = arr.get(a);
arr.set(a, arr.get(b));
arr.set(b, temp);
}
public ArrayList getSorted() {
ArrayList result = new ArrayList(this.items.size());
result.addAll(this.items);
int size = this.items.size();
for (int i = 0; i < size - 1; i++) {
swap(result, 0, size - 1 - i);
heapify(result, size - i - 1, 0, this.order);
}
return result;
}
}The classes in Java can be further improved for creating a real data structure that adds and removes elements. Currently it has been implemented just to wrap the heap and the sorting actually returns a copy. It is good enough for an example, though.
Conclusion
Heap sort is an nlogn sorting algorithm and the data structure behind it is useful for many other things than just sorting. It is one of my favourites, because it is really elegant. I hope this post was useful to you!
