In the last couple of years I have been using the Scala programming language for a large chunk of projects at work. I use it to write batch processing jobs with Spark, APIs using the Play Framework, different Akka programs as well as apps and tools. I’ve even written a book about design patterns in Scala in 2 editions.
Scala is an awesome programming language and I enjoy using it. It is very quick to write complex and efficient code. Of course, if you’re not careful or familiar enough with the language you might pay some price in terms of efficiency, but any programming language is like that. It is a multi-paradigm language that combines object-oriented and functional programming. It runs on the JVM and in theory it is compatible with Java and Java bytecode. And it practically is in most cases.
One day I was browsing around and I found Nayuki’s blog where he implemented an algorithm that finds the smallest enclosing circle of a number of points. The problem seemed like a really good candidate for a functional programming language, so I tried myself in porting his solution to Scala. Then I asked him if he is fine with me posting it here, and he was happy with it.
Adapted with permission from Nayuki’s source code.
The Code
Without digging too much in the problem, I will just show you the code here. For those of you, who are interested, please go to Nayuki’s page and you will see the resources he used for implementing the algorithm.
Point.scala
package com.ivan.nikolov.circles
import scala.math._
/**
* A class that represents a point in the 2d plain.
*
* Adapted with permission from Nayuki's source code
* (http://nayuki.eigenstate.org/page/smallest-enclosing-circle)
*/
case class Point(x: Double, y: Double) {
def subtract(point: Point): Point =
Point(x - point.x, y - point.y)
def distance(point: Point): Double =
hypot(x - point.x, y - point.y)
def cross(point: Point): Double =
x * point.y - y * point.x
def normal: Double = x * x + y * y
override def toString: String = "Point(x = %f; y = %f)".format(x, y)
}Circle.scala
package com.ivan.nikolov.circles
/**
* Adapted with permission from Nayuki's source code
* (http://nayuki.eigenstate.org/page/smallest-enclosing-circle)
*/
case class Circle(centre: Point, radius: Double) {
val EPSILON = 1e-12
def contains(point: Point): Boolean =
centre.distance(point) <= radius + EPSILON
def contains(points: Seq[Point]): Boolean =
points.forall(p => contains(p))
override def toString: String = "Centre: %s\nRadius: %f".format(centre.toString, radius)
}SmallestEnclosingCircle.scala
package com.ivan.nikolov.circles
import scala.util.Random
/**
* Adapted with permission from Nayuki's source code
* (http://nayuki.eigenstate.org/page/smallest-enclosing-circle)
*/
case class SmallestEnclosingCircle(points: Point*) {
def makeCircle: Circle = makeCircleShuffled(Random.shuffle(points))
private def makeCircleShuffled(shuffled: Seq[Point]): Circle =
shuffled.foldLeft((None: Option[Circle], 0))((agg, p) => {
val currCircle = agg._1
val index = agg._2
if (currCircle.isEmpty || !currCircle.get.contains(p)) {
(Some(makeCircleOnePoint(shuffled.slice(0, index + 1), p)), index + 1)
} else {
(currCircle, index + 1)
}
})._1.orNull
private def makeCircleOnePoint(pointsSeq: Seq[Point], point: Point): Circle =
pointsSeq.foldLeft((Circle(point, 0), 0))((agg, p) => {
val index = agg._2
val circle = if (agg._1.contains(p)) {
agg._1
} else agg._1.radius match {
case 0 => makeDiameterCircle(point, p)
case _ => makeCircleTwoPoints(pointsSeq.slice(0, index + 1), point, p)
}
(circle, index + 1)
})._1
private def makeCircleTwoPoints(pointsSeq: Seq[Point], p: Point, q: Point): Circle = {
val tmp = makeDiameterCircle(p, q)
if (tmp.contains(pointsSeq)) {
tmp
} else {
val leftAndRight = pointsSeq.foldLeft((None: Option[Circle], None: Option[Circle]))((agg, point) => {
var left = agg._1
var right = agg._2
val pq = q.subtract(p)
val cross = pq.cross(point.subtract(p))
val c = makeCircumCircle(p, q, point)
if (c != null) {
if (cross > 0 && (left.isEmpty || pq.cross(c.centre.subtract(p)) > pq.cross(left.get.centre.subtract(p)))) {
left = Some(c)
} else if (cross < 0 && (right.isEmpty || pq.cross(c.centre.subtract(p)) < pq.cross(right.get.centre.subtract(p)))) {
right = Some(c)
}
}
(left, right)
})
if (leftAndRight._2.isEmpty || leftAndRight._1.isDefined && leftAndRight._1.get.radius <= leftAndRight._2.get.radius) {
leftAndRight._1.orNull
} else {
leftAndRight._2.orNull
}
}
}
private def makeDiameterCircle(a: Point, b: Point): Circle =
Circle(Point((a.x + b.x) / 2, (a.y + b.y) / 2), a.distance(b) / 2)
private def makeCircumCircle(a: Point, b: Point, c: Point): Circle =
(a.x * (b.y - c.y) + b.x * (c.y - a.y) + c.x * (a.y - b.y)) * 2 match {
case 0 => null
case d: Double =>
val x = (a.normal * (b.y - c.y) + b.normal * (c.y - a.y) + c.normal * (a.y - b.y)) / d
val y = (a.normal * (c.x - b.x) + b.normal * (a.x - c.x) + c.normal * (b.x - a.x)) / d
val centre = Point(x, y)
Circle(centre, centre.distance(a))
}
}Demonstration
Nayuki has also done this javascript tool on his blog, which shows the algorithm functionality. I decided to play even more and I implemented a scala-swing application that draws the circle. It is worth a separate full article, so here I am just posting two pictures with examples:
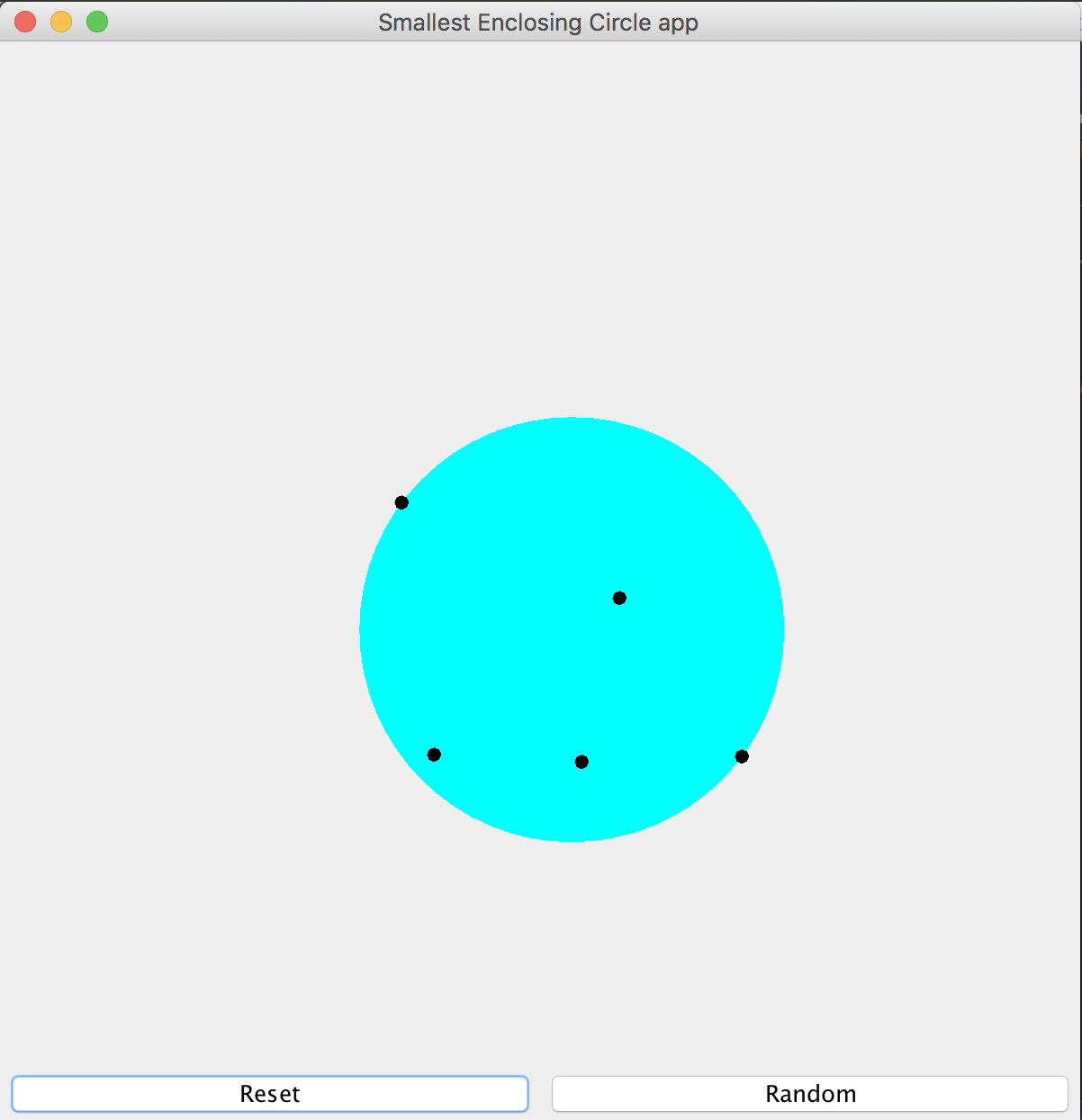
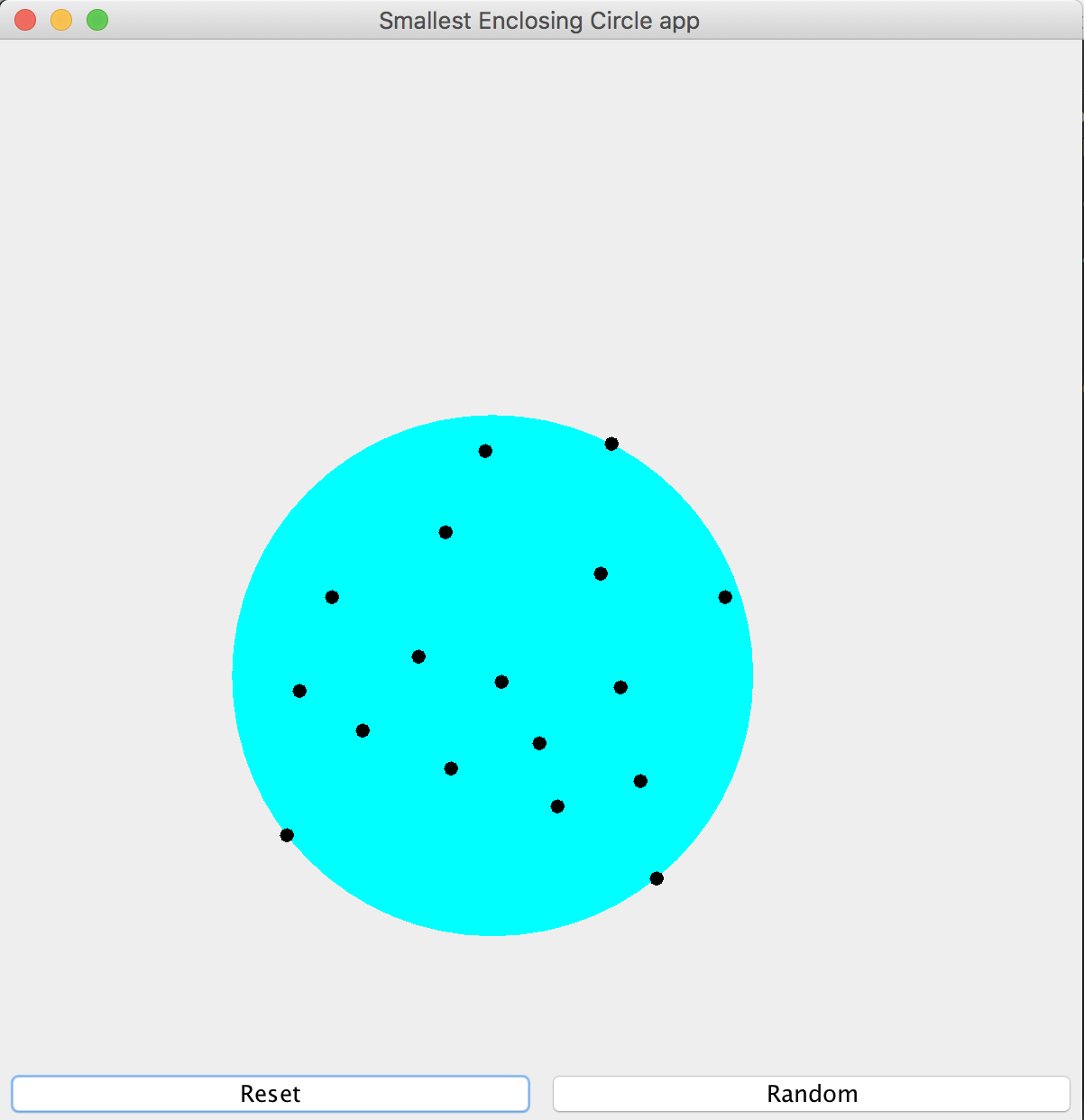
Conclusion
I hope the Scala implementation is useful to somebody. In order to keep the article short and clear, I haven’t spent time explaining what exactly I use from the language, but I guess you can look around and find out yourselves.
I also don’t claim that my solution is the best one. This is due to the specifics of Scala and the fact that one thing can be implemented in many different ways. I might comment on other specifics of the language and where I believe it should and should not be used in a separate article.
Finally, if you want to see my code, including the testing application, it is on my GitHub account: https://github.com/nikolovivan/scala_test.
